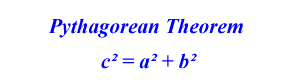Angles Within a Rectangle

Our SAT ACT Math Prep software program contains over 35 topic areas. One of them is Angles Within a Rectangle, and this page summarizes the main ideas of this topic. This page is intended for review, and is not a substitute for the interactive, self-paced tutorials of the MathTutor SAT ACT Math prep program.

General Explanation

Here are some important facts to know about right triangles:

A right triangle is a triangle in which one of the angles is 90 degrees. Look at the right triangle below:

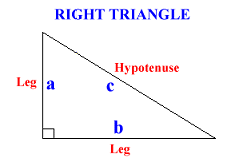
According to the Pythagorean Theorem, the three sides are related as follows:
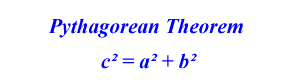
Here are some facts about angles of right triangles:
- The three angles in a triangle add up to 180 degrees.
- In a 30-60-90 triangle, or a triangle with 30, 60, and 90 degree angles, the sides will always be in a ratio of:
```
Short leg : Long leg: Hypotenuse = 1:√3:2
```
In a right triangle with angles of 45, 45, and 90 degrees, the two sides are of equal length.
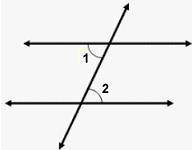
Finally, consider two parallel lines intersected by a diagonal line, called a transversal, below. Angle 1 and angle 2 are called alternate interior angles, and Angle 1 = Angle 2.

Sample Problem

You are a given a rectangle ABCD with diagonals AC and BD. The diagonals intersect at Point E and CD has length 1.

If angle BAC = 45 degrees, then what is the area of triangle CDE?

Solution

Angles DCA and BAC are alternate interior angles, and therefore are equal. Since angle BAC = 45 degrees, then angle DCA = 45 degrees.

Since angle DCA = 45 degrees and CD = 1, then it follows that AD = 1 and AC = √2.

Since the diagonals bisect each other, CE = 1/2 * CA = 1/2 * 2.

It can be shown that the area of triangle CDE is 1/2 the area of triangle ADC. Therefore:

Area of triangle CDE = 1/2 * area of triangle ACD

= 1/2 * 1/2 * base * height

= 1/2 * 1/2 * length of CD * length of AD

= 1/2 * 1/2 * 1 * 1

= 1/4

MathTutor Home

SAT ACT Math Prep Software
Product Page