Coordinate Geometry

Our SAT ACT Math Prep software program contains over 35 topic areas. One of them is Coordinate Geometry, and this page summarizes the main ideas of this topic. This page is intended for review, and is not a substitute for the interactive, self-paced tutorials of the MathTutor SAT ACT Math prep program.

General Explanation

This problem tests your general understanding of coordinate geometry. The following information is needed to solve these problems:

Two points on the same vertical line have the same x-coordinate. Two points on the same horizontal line have the same y-coordinate.
The value of the x-coordinate of a point increases as the point moves to the right. The value of the y-coordinate of a point increases as the point moves upward.

In addition to the concept of coordinates, this problem type also uses the concept of the midpoint of a line. The following two facts are needed to solve some of the problems:
The coordinates of the midpoint of a line segment connecting two points can be determined by taking the average of the x-coordinates and the average of the y-coordinate of the two points. That is, if the coordinates of point 1 are (x₁, y₁), and the coordinates of point 2 are (x₂, y₂), then the coordinates of the midpoint o the line segment connecting point 1 and point 2 - denoted as (x_m, y_m) - are as follows:
```
x_m = (x₁ + x₂) / 2 
y_m = (y₁ + y₂) / 2
```
The diagonals of a parallelogram bisect each other. That is, the place where the two diagonals intersect is the midpoint of both of the diagonals. A rectangle is an example of a parallelogram, so a rectangle has this property.

In these problems, you should start by finding the coordinates of all four corners of the given rectangle (or as many as you will need). Then you can proceed to find any midpoints that you would need to solve the problem.

Sample Problem

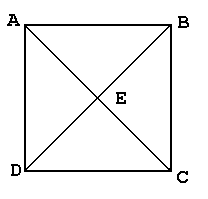
You are given rectangle ABCD with diagonals AC and BD. The diagonals intersect at point E.

The coordinates of D are (0,3).
The coordinates of B are (6,7).

Find the coordinates of the midpoint of AB.

Solution

Since point A is on the same vertical line as point D, it must have the same (x-coordinate as D. Since it is on the same horizontal line as point B, it must have the same y-coordinate as B. Therefore, the coordinates of A are (0,7). We could similarly work out the coordinates of C (which are (6,3)), though they are not needed in this problem.

We are asked to find the midpoint of AB. We do this by using the midpoint formula. Starting with the coordinates of A and B:

A = (0,7), so x₁ = 0 and y₁ = 7
B = (6,7), so x₂ = 6 and y₂ = 7
So, x_m = (0 + 6) / 2 = 3 and y_m = (7 + 7) / 2 = 14

So the coordinates of the midpoint of AB are (3, 7).

MathTutor Home

SAT ACT Math Prep Software
Product Page