Geometry Self-Study Software
Product Page

Arcs and Angles

Our Geometry tutorial software program contains over 40 topic areas. One of them is Arcs and Angles, and this page summarizes the main ideas of this topic. This page is intended for review, and is not a substitute for the interactive, self-paced tutorials of the MathTutor geometry software program.

General Explanation

To solve problems involving triangles within circles, like the one shown below:

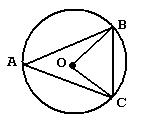
these facts should be kept in mind:

The measure of a central angle is the same as the measure of the arc it cuts off. Therefore, Angle BOC = arc BC.
The measure of an inscribed angle is half the measure of the arc it cuts off. Therefore, Angle BAC = arc BC / 2.
A total circle contains 360 degrees. In the picture above, arc BC + arc CA + arc AB = 360°. You should also recall that the angles of a triangle add up to 180 degrees.
All radii of a circle are the same length.
Two chords of a circle will be the same length if and only if the arcs they cut off are congruent. In the picture above, if AB = AC, then arc AB = arc AC.

Sample Problem

A triangle with vertices A, B, and C is inscribed in a circle with center 0
and radius 1.

Suppose AB = AC and that Angle BAC = 100°.

Find the measure of Angle CBO.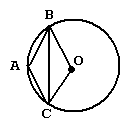

Solution

The only angle we are given is Angle BAC. Since it is an inscribed angle, its measure is half that of the arc it cuts off. Arc BC therefore must have twice the measure of Angle BAC, so arc BC = 200°.

Because there are 360 degrees in a circle, Arc BC + arc BAC = 360°. Since arc BC = 200°, arc BAC must equal 160°.

Angle BOC is a central angle, and so must be the measure of the angle it cuts off. Therefore, Angle BOC = arc BAC = 160°.

Since BO and CO are both radii, BO = CO. The triangle they form is isosceles, so Angle BCO = Angle CBO.

We know one of the angles of triangle BOC and that the other two angles are the same. If we let x be one of the other two angles, then x + x + 160° = 180°. Solving this equation, we get x = 10°, so the answer is 10 degrees.

MathTutor Home

Geometry Self-Study Software
Product Page