The Derivative

In this lesson we wil learn about the DERIVATIVE, one of the most important concepts in calculus. One of the goals of calculus is to measure the rate at which quantities are growing or changing. More precisely, we want to determine how much one variable will change in response to a change in another variable.
 
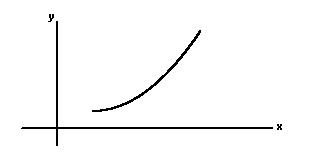
Here's another way of saying it: Let's say the variable 'y' is a function of the variable 'x'. If x changes by a certain amount, say Δx, then y will change by an amount Δy. The ratio of the change in y (which is Δy) to the change in x (Δx) tells us the rate at which y changes in response to a change in x.
 
Let's consider a case in which y is a linear function of x. In this case the graph showing the relationship of y and x is a straight line. The steepness of this line is a measure of how quickly y changes in response to a change in x. Another name for the steepness of a straight line is SLOPE. Slope is defined as the change in y divided by the change in x. If the slope of a straight line is 3, this means that if x is increased by one, then y will increase by three. A straight line has constant slope at all points along the line. So regardless of the value of x, y will change at the same rate with respect to x.
 
But what about cases where the graph of x and y is not a straight line, but is a curve? How do we measure the steepness or slope of a curve?
 
Look at the graph below. We can see that the slope of the curve is different at different points.

To find the slope of this curve at a particular point let's do this: Let's calculate the slope (rate of change) of the function between that point (a) and a nearby point (b). Then let's move b closer and closer to a and determine what value the slope is approaching. The average rate of change from point a to point b is:

 

   f(b) - f(a)
              
      (b-a)

 

If we define Δx as (b-a), our formula becomes:

 

   f(a+Δx) - f(a)
                 
          Δx

 

As Δx gets smaller and smaller, the slope approaches a limiting value, which we can represent as follows:

 

     f(a+Δx) - f(a)
lim                
Δx→0       Δx

 

The notation

 

lim 
Δx→0

 

is read "the limit as Δx approaches zero".
 
The slope of the function y=f(x) at the point "x" is called the DERIVATIVE. It is also commonly written as dy/dx.